Todo conjunto numérico é expresso por uma letra (IN, Z, IR, ...), caso essa letra venha com um asterisco sobrescrito, deste conjunto se exclui o zero (0), se vier um sinal de mais (+) subscrito, deste conjunto se excluem os números negativos e se vier um sinal de menos ( – ) subscrito, deste conjunto se excluem os números positivos.
Números Naturais
É formado pela cardinalidade dos conjuntos. São todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula N; Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar um * ao lado do N:
N = {0,1,2,3,4,5,6,7,8,9,10, ...}
N* = {1,2,3,4,5,6,7,8,9,10,11, ...}
Números Inteiros
É formado pelos números naturais juntamente com os inteiros negativos.
Z = {... -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}
O conjunto dos inteiros possui alguns subconjuntos, eles são:
- Inteiros não negativos
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao conjunto dos números naturais.
É representado por Z+:
Z+ = {0,1,2,3,4,5,6, ...}
- Inteiros não positivos
São todos os números inteiros que não são positivos. É representado por Z-:
Z- = {..., -5, -4, -3, -2, -1, 0}
- Inteiros não negativos e não-nulos
É o conjunto Z+ excluindo o zero. Representa-se esse subconjunto por Z*+:
Z*+ = {1, 2, 3, 4, 5, 6, 7, ...}
Z*+ = N*
- Inteiros não positivos e não nulos
São todos os números do conjunto Z- excluindo o zero. Representa-se por Z*-.
Z*- = {... -4, -3, -2, -1}
Números Racionais
Incluem-se neste conjunto os números inteiros, os decimais exatos (finitos) e as dízimas periódicas (infinitas com repetição de decimais; que repete uma sequência de algarismos da parte decimal infinitamente, como "12,050505..."). Todo número racional pode ser escrito na forma a / b.
Números Irracionais
É formado pelas dízimas não-periódicas. Os números irracionais não podem ser expressos na forma a / b. Exemplo:
Obs: Um número jamais poderá ser racional irracional ao mesmo tempo. Ou seja, os conjuntos Q e I não possuem elementos em comum.
Números Reais
Inclui todos os conjuntos anteriormente citados.Os únicos números que não fazem parte deste conjunto são as raízes de índices pares de números negativos.
Obs: Apenas dois tipos de números não são reais, são eles as raízes de índice par de números negativos e o resultado de uma divisão por zero.
Números Imaginários
No conjunto dos números reais ( IR ) 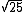 a é igual a 5, mas qual é a
a é igual a 5, mas qual é a 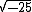 ?
?
Como sabemos, não existe a raiz quadrada real de um radicando negativo com índice par. No conjunto dos números reais o máximo que podemos fazer é simplificar o radical desta forma:
Ainda assim o fator 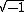 não é um número real, pois o radicando -1 é um número negativo.
não é um número real, pois o radicando -1 é um número negativo.
Para maiores informações sobre como retiramos o número 5 do radical, você pode consultar o nosso artigo sobre isso a radiciação e suas propriedades.
Números Complexos
De forma semelhante os números complexos podem ser representados por meio de uma expressão algébrica:
Sendo a e b números reais e i a unidade imaginária.
a é a parte real do número complexo z e bi é a sua parte imaginária.
Definimos o conjunto dos números complexos como:
O conjunto dos números reais ( 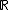 ) e o conjunto dos números imaginários (
) e o conjunto dos números imaginários ( 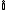 ) são subconjuntos do conjunto dos números complexos (
) são subconjuntos do conjunto dos números complexos ( 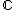 ). Em função disto um número complexo pode ser imaginário, imaginário puro ou real.
). Em função disto um número complexo pode ser imaginário, imaginário puro ou real.
Fonte: http://www.tutorbrasil.com.br/estudo_matematica_online/conjuntos/conjuntos
http://www.matematicadidatica.com.br/ConjuntoNumerosComplexos.aspx
http://www.infoescola.com/matematica/conjuntos-numericos/
http://www.matematicanoenem.com.br/ .pdf



Nenhum comentário:
Postar um comentário